بعد از نوشتن و انتشار این فعالیت، بازخوردهایی به آن داده شد که سبب شد با اندکی تغییر تحت عنوان «ارزشمکانی لوبیایی ۲» بازنویسی شود. از آنجا که این دو فعالیت بسیار شبیه هم هستند، پیشنهاد میکنیم که به «ارزشمکانی لوبیایی ۲» هم سری بزنید و به اقتضای نیاز کلاس خود نسخهی مناسبتر را انتخاب کنید.
ارزشمکانی لوبیایی ۱: بازیگونهتر است، تنوع پاسخهایش میتواند فرصت آزمون و خطا به کودک بدهد، برای تمرین جمع سودمند است.
ارزشمکانی لوبیایی ۲: مسیر شفافتری را برای تجربهی ارزشمکانی در پیش میگیرد و راحتتر به جدول ارزشمکانی متصل میشود.
چیزی که در اولین مواجهههای کودک با ارزشمکانی چالش ایجاد میکند، این است که ارقامی که در هر کدام از جایگاههای ارزشمکانی قرار میگیرند، عیناً نمایانگرِ مقدار خود نیستند.
مثلاً عددِ ۱۲۷ را در نظر بگیرید:
رقم ۲ در جایگاه دهگان و ۱ در جایگاه صدگان قرار دارد. اما ۲ نمایانگرِ ۲۰ (یا همان ۲ دهتایی) و ۱ نمایانگرِ ۱۰۰ (یا همان ۱ صدتایی) است. در واقع جایگاهِ قرار گرفتنِ ارقام سبب میشود که ارزشِ ویژهای به هر کدام از آنها داده شود.
این تجربه برای کودک تازه است و اوایل کار ممکن است چالشی برای او ایجاد کند.
فعالیتِ پیشِ رو بازی بسیار سادهایست. این بازی کمک میکند که کودک ابتدا مفهوم ارزشمکانی را در جایی خارج از دنیای اعداد تجربه کند. بنابراین این بازی در کلاس اول و پیش از مواجهه با ارزشمکانیِ اعداد مناسب است.






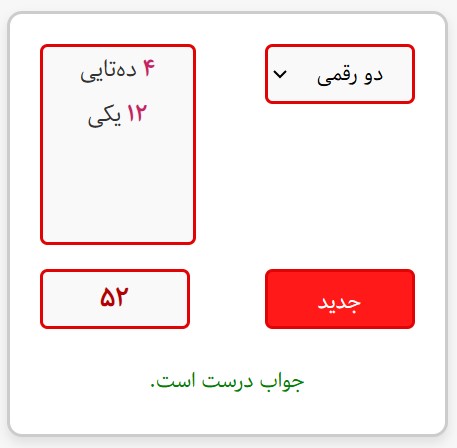









خب، خب، باید اعتراف کنم اول به نظرم خیلی هیجان انگیز آمد. بعد یهو به خودم آمدم و دیدم این یه نسخه مستطیلی شده از دارت است ? ولی بعد دوباره بیشتر به خودم آمدم و دیدم این نسخه مستطیلی شده چقدر راحت تر میشه به ارزش مکانی پیوند بخوره. کافیه بازی را با یک مستطیل دراز انجام داد که مثلا یک در دو است، برای عددهای دو رقمی، یا یک در سه است برای عددهای سه رقمی. جالبه که این کمک میکنه بچه ها متوجه بشوند که در عدد نویسی مجبور هستند یه قرار داد مربوط به جهت داشته باشند. فرض کنید لوبیاها را ریختیم روی یک مستطیل یک در دو. فرض کنید ارزش یکی از خانه ها ۱ است و ارزش آن یکی ده. حالا فرض کنید روی خانه یکی، سه لوبیا افتاده و روی خانه دهی، دو لوبیا. حالا میخواهیم این را بنویسیم یه جوری که همه اطلاعات لازم را داشته باشه. اینکه فقط بنویسیم دو سه کار نمیکنه.باید یه قرارداد اضافی هم داشته باشیم که دو را کجا بنویسیم، سه را کجا
مرسی. موافقم. این پیشنهاد رو پیاده میکنیم.
ببینید با این پیشنهاد موافقید:
برای پلهی بعد از این فعالیت میشه مستطیل یک در دو باشد با ارزشِ ۱ و ۱۰. اما به جای لوبیا، تاس بریزیم و عدد نوشته شده روی تاس مشخص کند که چند تا ۱۰ تایی و چند تا یکی باید امتیاز بگیرد.
آره ایده خوبیه. هم تمیزتر است و هم به ریاضیات ماجرا نزدیکتر